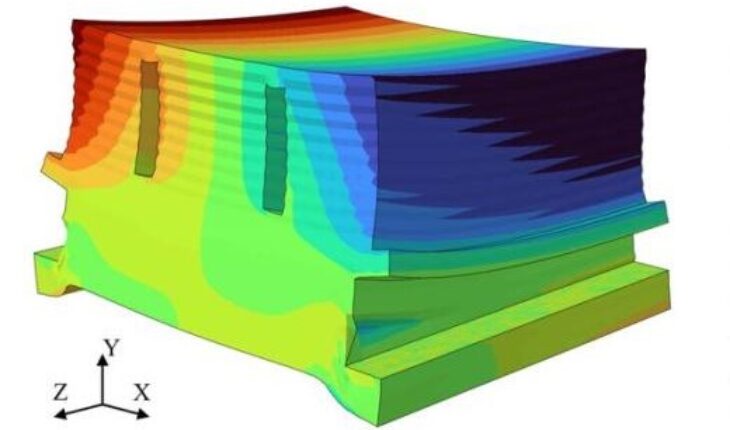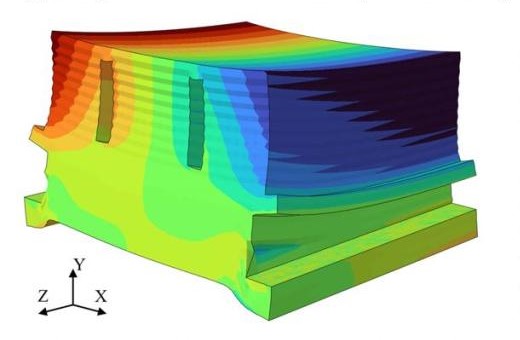
Residual stress is a frequent issue for additive manufacturing, but simulation can help address it.
In 3D printed parts, residual stress buildup can result in cracking, making it a costly error in terms of both time and materials. Despite being a well-known problem in additive manufacturing (AM), residual stress is still poorly understood and often difficult to determine, especially in anisotropic materials. Although there are simplified ways of generating rough estimations of residual stresses in 3D printed parts, simulation remains the key to predicting and compensating for residual stress in additive manufacturing.
How do you calculate residual stress in additive manufacturing?
Given the physics involved in fusion-based 3D printing processes, the simplest formula for estimating residual stress would be based on thermal strains and the temperature differential during the cooling phase. For example:
σres = EαΔT
Where:
- E = Young’s Modulus (Pa)
- α = Coefficient of thermal expansion (1/K)
- ΔT = Temperature change, typically the difference between ambient and peak process temperature (K)
Although it may be useful as a first-order approximation, this formula involves a gross oversimplification of the additive process, discounting cyclic heating, localized cooling and the effects of anisotropy, among other factors.
Ideally, what’s needed to estimate residual stress in an AM part is a finite-element-based stress tensor equation, such as the following:
∇⋅σ+ƒ = 0, σ = D : (ε−εthermal)
Where:
- ∇⋅σ = Divergence of the stress tensor (Pa/m)
- ƒ = Body force vector (N/M3)
- D = Material stiffness matrix
- ε = Total strain tensor
- εthermal = Thermal strain tensor
This formula is part of a system of coupled equations used in finite element analysis (FEA) to model thermal, mechanical and phase-change behaviors in 3D printed parts. As such, it requires a detailed knowledge of material properties, boundary conditions and a part’s thermal history.
How is residual stress evaluated in 3D printed parts?
There are numerous methods for assessing residual stress in AM parts, both destructive and non-destructive. These include x-ray and neutron diffraction, ultrasonic velocity measurements, magnetoacoustic emissions, hole-drilling, tool-point indentation, crack pliability assessments, layer removal and electron speckle interferometry.
In an experimental context, residual stress can be evaluated using the so-called bridge curvature method. This approach begins with printing a bridge-shaped test part. When separated from the build plate, the internal residual stresses partially relax, causing the specimen to curl at a certain angle. By measuring this curling, engineers and materials scientists can collect information about the residual stresses resulting from a particular combination of additive materials and processes.
What printing parameters affect residual stress?
With regard to polymer 3D printing, the crystallization of semi-crystalline polymers strongly depends on temperature and hence on print parameters. For example, increasing nozzle speed can reduce the cooling time between applied layers, which can negatively affect the crystallinity of the polymer and reduce overall tensile strength.
In addition, raster pattern also has a direct impact on part strength, print time and the accumulated stresses that can cause cracking or delamination. Generally, a concentric raster pattern yields the lowest residual stress and hence the lowest deformation. There’s also an inverse relationship between layer thickness, printing speed and the level of residual stresses, i.e., thinner layers and faster speeds tend to increase residual stress.
For these reasons, simulating the process, mechanics and thermal phenomena involved in 3D printing can help engineers optimize both 3D printing time and material usage by identifying regions of a part that may require additional support materials, rounded fillets or 45-degree chamfers.